Αριθμητικά συστήματα και όροι

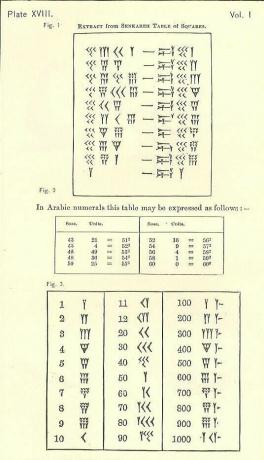
Τρεις κύριες περιοχές διαφοράς από τους αριθμούς μας

Φανταστείτε πόσο εύκολο θα ήταν να μάθετε αριθμητικά τα πρώτα χρόνια αν το μόνο που έπρεπε να κάνετε ήταν να μάθετε να γράφετε μια γραμμή όπως εγώ και ένα τρίγωνο. Αυτό είναι βασικά όλοι οι αρχαίοι άνθρωποι της Μεσοποταμίας έπρεπε να κάνουν, αν και τα διαφοροποιούσαν εδώ και εκεί, επιμηκύνοντας, στρέφοντας, κλπ.

Δεν είχαν τα στυλό και τα μολύβια μας, ούτε χαρτί για αυτό το θέμα. Αυτό που έγραψαν ήταν ένα εργαλείο που θα χρησιμοποιούσε στη γλυπτική, αφού το μέσο ήταν πηλός. Είτε αυτό είναι πιο δύσκολο είτε πιο εύκολο να μάθει κανείς να χειριστεί από ό, τι ένα μολύβι είναι μια πεσέτα, αλλά μέχρι στιγμής είναι μπροστά στο τμήμα ευκολίας, με μόνο δύο βασικά σύμβολα για μάθηση.

Το επόμενο βήμα ρίχνει ένα κλειδί στο τμήμα απλότητας. Χρησιμοποιούμε α Βάση 10, μια έννοια που φαίνεται προφανής αφού έχουμε 10 ψηφία. Στην πραγματικότητα έχουμε 20, αλλά ας υποθέσουμε ότι φορούμε σανδάλια με προστατευτικά καλύμματα toe για να κρατήσουμε την άμμο μέσα την έρημο, ζεστό από τον ίδιο ήλιο που θα ψήριζε τα πηχάκια και θα τα διατηρούσε για να βρούμε χιλιετίες αργότερα. Οι Βαβυλώνιοι χρησιμοποίησαν αυτή τη Βάση 10, αλλά μόνο εν μέρει. Εν μέρει χρησιμοποίησαν τη Βάση 60, τον ίδιο αριθμό που βλέπουμε γύρω μας σε λεπτά, δευτερόλεπτα και βαθμούς τριγώνου ή κύκλου. Ήταν κατακτημένοι αστρονόμοι και έτσι ο αριθμός θα μπορούσε να προέλθει από τις παρατηρήσεις τους για τους ουρανούς. Η Βάση 60 έχει επίσης διάφορους χρήσιμους παράγοντες που την καθιστούν εύκολο να υπολογίσετε με. Ακόμα, η ανάγκη να μάθετε τη Βάση 60 είναι εκφοβιστική.

Στο "Αφιέρωμα στη Βαβυλωνία" [Η Μαθηματική Εφημερίδα, Vol. 76, Νο. 475, "Χρήση της Ιστορίας των Μαθηματικών στη Διδασκαλία των Μαθηματικών" (Μαρ., 1992), σελ. 158-178], ο συγγραφέας-δάσκαλος Nick Mackinnon λέει ότι χρησιμοποιεί τα Βαβυλωνιανά μαθηματικά για να διδάξει τα 13χρονα για βάσεις άλλες από 10. Το σύστημα της Βαβυλώνας χρησιμοποιεί τη βάση-60, που σημαίνει ότι αντί να είναι δεκαδικό, είναι σεζόν.

Τόσο το σύστημα των Βαβυλωνίων όσο και το δικό μας στηρίζονται στη θέση να δίνουν αξία. Τα δύο συστήματα το κάνουν με διαφορετικό τρόπο, εν μέρει επειδή το σύστημά τους δεν είχε μηδέν. Η εκμάθηση του συστήματος θέσης της Βαβυλωνίας από αριστερά προς τα δεξιά (υψηλή προς χαμηλή) για πρώτη γεύση της βασικής αριθμητικής δεν είναι πιθανόν πλέον δύσκολο από το να μάθουμε το 2-κατευθυντικό μας, όπου πρέπει να θυμόμαστε τη σειρά των δεκαδικών αριθμών - αυξάνοντας από το δεκαδικό, δεκάδες, εκατοντάδες, και στη συνέχεια εκκενώνοντας προς την άλλη κατεύθυνση από την άλλη πλευρά, δεν υπάρχει στήλη, μόνο δέκατα, εκατοστά, χιλιάδες, κλπ.

Θα μπω στις θέσεις του Βαβυλωνιακού συστήματος σε άλλες σελίδες, αλλά πρώτα υπάρχουν μερικές σημαντικές λέξεις για να μάθουν.

Μιλάμε για περιόδους ετών χρησιμοποιώντας δεκαδικές ποσότητες. Έχουμε μια δεκαετία για 10 χρόνια, έναν αιώνα για 100 χρόνια (10 δεκαετίες) ή 10Χ10 = 10 χρόνια τετράγωνο, και μια χιλιετία για 1000 χρόνια (10 αιώνες) ή 10Χ100 = 10 χρόνια cubed. Δεν ξέρω κανένα ανώτερο όρο από αυτό, αλλά αυτές δεν είναι οι μονάδες που χρησιμοποίησαν οι Βαβυλώνιοι. Ο Νίκος Mackinnon αναφέρεται σε ένα δισκίο από το Senkareh (Larsa) από τον Sir Henry Rawlinson (1810-1895) * για τις μονάδες που χρησιμοποίησαν οι Βαβυλώνιοι και όχι μόνο για τα χρόνια που συμμετείχαν, αλλά και για τις ποσότητες που υπονοούσαν:

1. soss
2. ner
3. sar.

sossnersosssarsoss

Ακόμα δεν υπάρχει tie-breaker: Δεν είναι απαραίτητα ευκολότερο να μαθαίνετε τετραγωνισμένους και cubed όρους που προέρχονται από το έτος από τα λατινικά, από ό, τι είναι ένα συλλαλικό Βαβυλωνιανό που δεν περιλαμβάνει κύβους, αλλά πολλαπλασιασμό 10.

Τι νομίζετε; Θα ήταν δυσκολότερο να μάθετε τα βασικά του αριθμού ως παιδί της Βαβυλώνας ή ως σύγχρονος φοιτητής σε αγγλόφωνο σχολείο;

* Ο George Rawlinson (1812-1902), ο αδελφός του Henry, παρουσιάζει έναν απλοποιημένο μεταγραμμένο πίνακα τετραγώνων Οι Επτά Μεγάλες Μονάρχες του Αρχαίου Ανατολικού Κόσμου. Ο πίνακας φαίνεται να είναι αστρονομικός, με βάση τις κατηγορίες των Βαβυλωνίων χρόνων.

Όλες οι φωτογραφίες προέρχονται από αυτήν την online σαρωμένη έκδοση μιας έκδοσης του George Rawlinson του 19ου αιώνα Οι επτά μεγάλες μονάρχες του αρχαίου ανατολικού κόσμου.

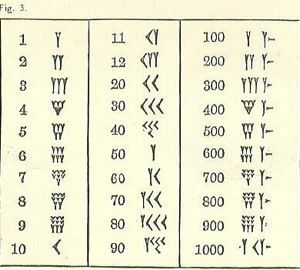
Από τότε που μεγάλαμε με ένα διαφορετικό σύστημα, οι αριθμοί της Βαβυλώνας είναι συγκεχυμένοι.

Τουλάχιστον οι αριθμοί τρέχουν από ψηλά προς τα αριστερά προς χαμηλά στα δεξιά, όπως το αραβικό μας σύστημα, αλλά τα υπόλοιπα μοιάζουν πιθανότατα άγνωστα. Το σύμβολο για ένα είναι σφήνα ή μορφή σχήματος Υ. Δυστυχώς, το Y αντιπροσωπεύει επίσης ένα 50. Υπάρχουν μερικά ξεχωριστά σύμβολα (όλα με βάση τη σφήνα και τη γραμμή), αλλά όλοι οι άλλοι αριθμοί σχηματίζονται από αυτούς.

Θυμηθείτε τη μορφή της γραφής είναι σφηνοειδής ή σφηνοειδούς σχήματος. Λόγω του εργαλείου που χρησιμοποιείται για την κλήρωση των γραμμών, υπάρχει μια περιορισμένη ποικιλία. Η σφήνα μπορεί να έχει ή να μην έχει ουρά, τραβηγμένη τραβώντας την γραφίδα σφηνοειδούς γραφής κατά μήκος του πηλού μετά την αποτύπωση της μορφής τριγωνικού τμήματος.

Τα 10, τα οποία περιγράφονται ως βέλος, μοιάζουν με λίγο σαν

Τρεις σειρές έως 3 μικρών 1s (γράφονται όπως Ys με μερικές βραχύτερες ουρές) ή 10s (ένα 10 είναι γραμμένο σαν

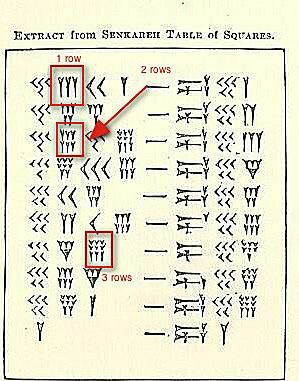
Υπάρχουν τρεις σειρές αριθμών σφηνοειδούς συστοιχίες που επισημαίνονται στην παραπάνω εικόνα.

Αυτή τη στιγμή δεν ασχολούμαστε με την αξία τους, αλλά με την επίδειξη του τρόπου που θα βλέπατε (ή γράφετε) οπουδήποτε από 4 έως 9 του ίδιου αριθμού ομαδοποιημένου. Τρεις πηγαίνουν στη σειρά. Εάν υπάρχει ένα τέταρτο, πέμπτο ή έκτο, πηγαίνει κάτω. Εάν υπάρχει έβδομο, όγδοο ή ένατο, χρειάζεστε μια τρίτη σειρά.

Οι παρακάτω σελίδες συνεχίζονται με οδηγίες σχετικά με τους υπολογισμούς με την Βαβυλωνιακή σφηνοειδή.

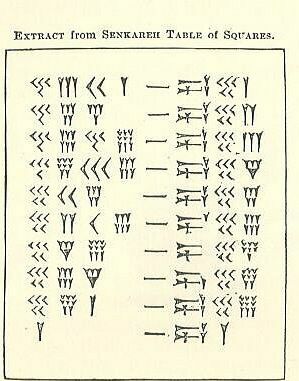
Από αυτά που έχετε διαβάσει παραπάνω για το soss - που θα θυμάστε είναι ο Βαβυλωνιανός για 60 χρόνια, η σφήνα και το βέλος - που είναι περιγραφικά ονόματα για σφηνοειδή σημάδια, δείτε αν μπορείτε να καταλάβετε πώς αυτοί οι υπολογισμοί λειτουργούν. Η μία πλευρά του σημείου που μοιάζει με παύλα είναι ο αριθμός και ο άλλος είναι το τετράγωνο. Δοκιμάστε το ως ομάδα. Εάν δεν μπορείτε να το καταλάβετε, δείτε το επόμενο βήμα.

Μπορείτε να το καταλάβετε τώρα; Δώστε την ευκαιρία.

...

Υπάρχουν 4 καθαρές στήλες στην αριστερή πλευρά ακολουθούμενες από μια πινακίδα και 3 στήλες στα δεξιά. Εξετάζοντας την αριστερή πλευρά, το ισοδύναμο της στήλης 1s είναι στην πραγματικότητα οι 2 στήλες που βρίσκονται πιο κοντά στην "παύλα" (εσωτερικές στήλες). Οι άλλες 2, οι εξωτερικές στήλες υπολογίζονται μαζί στη στήλη των 60s.

• Το 4-
• Τα 3-Ys = 3.
• 40+3=43.
• Το μόνο πρόβλημα εδώ είναι ότι υπάρχει ένας άλλος αριθμός μετά από αυτούς. Αυτό σημαίνει ότι δεν είναι μονάδες (η θέση τους). Τα 43 δεν είναι 43-αυτά, αλλά 43-60, δεδομένου ότι είναι το σύστημα sexagesimal (βάση-60) και είναι στο soss όπως υποδεικνύει ο κατώτερος πίνακας.
• Πολλαπλασιάστε 43 με 60 για να πάρετε 2580.
• Προσθέστε τον επόμενο αριθμό (2-
• Τώρα έχετε 2601.
• Αυτό είναι το τετράγωνο του 51.

Η επόμενη σειρά έχει 45 στο soss στήλη, ώστε να πολλαπλασιάσετε 45 με 60 (ή 2700), και στη συνέχεια να προσθέσετε τη στήλη 4 από τις μονάδες, ώστε να έχετε 2704. Η τετραγωνική ρίζα του 2704 είναι 52.

Μπορείτε να καταλάβετε γιατί ο τελευταίος αριθμός = 3600 (60 τετράγωνο); Συμβουλή: Γιατί δεν είναι 3000;